As part of the "Smart Campus" initiative at UMT University, a senior student team is digitising every engineering blueprint of the underground infrastructure. After scanning the legacy drawings, they recovered a large collection of straight-line segments-each one representing a stretch of pipe, buried cable, or power line. Because different construction crews often redrew the same objects, many of these segments lie on the same infinite line and overlap one another wholly or partially.

To simplify the blueprint, the team must keep the minimum number of distinct segments that still preserves all information. Two segments are said to overlap if they lie on the same straight line and have an intersection of positive length.

Input

The input consists of multiple test cases. Each test case begins with an integer ~n (1 ≤ n ≤ 10^4)~ - the number of line segments in the map.

Then follow n lines, each containing 4 real numbers: ~x_1, y_1, x_2, y_2~ which represent the two endpoints of a line segment.

• Coordinates are in the range [0, 1000], with up to 2 decimal places.

• No segment has zero length.

• The input ends with a line containing a single 0 - this line should not be processed.

Output

For every test case, output a single line with one integer - the minimum number of distinct segments that must remain.

Sample Input 1

3
1.0 10.0 3.0 14.0
0.0 0.0 20.0 20.0
10.0 28.0 2.0 12.0
2
0.0 0.0 1.0 1.0
1.0 1.0 2.15 2.15
2
0.0 0.0 1.0 1.0
1.0 1.0 2.15 2.16
0

Sample Ouput 1

2
1
2

During a joint cybersecurity exercise at UMT University, two student agents-codenamed An and Khang-communicate through an unusual zigzag columnar transposition. Given a positive integer M (the number of columns), the sender writes the plaintext into a rectangle row by row:

• Even-numbered rows (0, 2, 4, . . . ) are filled left → right.

• Odd-numbered rows (1, 3, 5, . . . ) are filled right → left.

If the last row is incomplete, random lowercase letters are appended until the rectangle is full. Finally, the ciphertext is produced by reading the rectangle column by column, top → bottom, left → right.

Your task is to reverse this process: given M and the ciphertext, reconstruct the original rectangle and output the plaintext (including any padding letters exactly as sent).

Input

The input consists of multiple test cases. Each test case contains two lines:

• The 1st line contains a single integer ~M~ ~(2 ≤ M ≤ 20)~ - the number of columns.

• The 2nd line contains a string of lowercase letters (maximum length is 200) - ciphertext.

The input ends with a line containing a single 0. This line should not be processed.

Output

For every test case, print a single line containing the recovered plaintext (padding included, no spaces).

Sample Input 1

5
toioynnkpheleaigshareconhtomesnlewx
3
ttyohhieneesiaabss
0

Sample Ouput 1

theresnoplacelikehomeonasnowynightx
thisistheeasyoneab

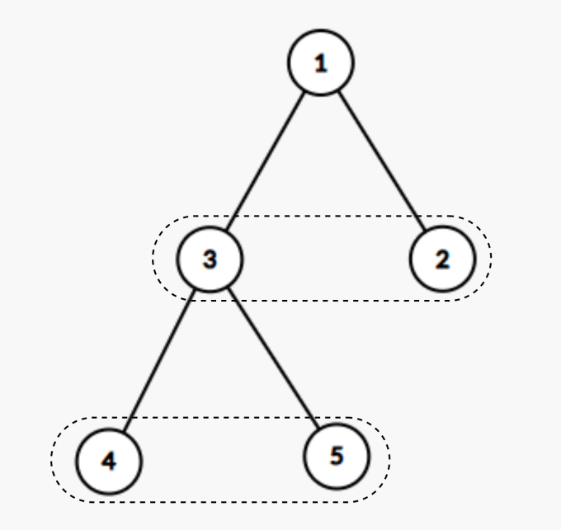
In a gamified data-structures lab at UMT University, students model the campus network as a rooted tree. Every node initially holds 0 coins. During the experiment they must process ~M~ operations of two types:

• Type 1 - mass deposit 1 L Y: add ~Y~ coins to every node whose distance from the root is exactly ~L~.

• Type 2 - query subtree 2 X: output the total number of coins currently stored in the subtree rooted at node ~X~.

Your task is to efficiently support these operations and output the result for each Type 2 query.

Input

Input The first line contains two integers ~N~ and ~M~ ~(1 ≤ N ≤ 10^5, 1 ≤ M ≤ 10^4)~ - the number of nodes and the number of operations.

The next ~N~ - 1 lines contain each two integers u, v that denote an edge between the nodes ~u~ and ~v~.

The next ~M~ lines each describe a query:

• Type 1: ~1~ ~L~ ~Y~ - add ~Y~ coins to all nodes at depth ~L~ from the root.

• Type 2: ~2~ ~X~ - output the total coins in the subtree of node ~X~.

The tree is undirected but rooted at node 1. The input guarantees a valid tree.

Output

For each query of Type 2, output the corresponding sum on a separate line.

Constraints

• 0 ≤ ~L~ ≤ maximum height of the tree

• 0 ≤ ~Y~ ≤ ~10^9~

• 1 ≤ ~X~, ~u~, ~v~ ≤ ~N~

Sample Input 1

5 4
1 2
1 3
3 4
3 5
1 1 2
1 2 3
2 3
2 1

Sample Ouput 1

8
10

At UMT University's annual Code & Conquer tournament, competitors design algorithms for fantasy battles. Your avatar, the warrior Ba Hong, must defeat a horde of n monsters with his enchanted axe Warcry. Each swing works as follows:

• The targeted monster loses exactly ~p~ hit-points.

• Every other monster simultaneously loses exactly ~q~ hit-points ~(q ≤ p)~ from the shock-wave.

If any monster's hit points become non-positive, it is considered slain. Ba Hong can choose the target of each swing and wishes to minimize the total number of axe strikes required to defeat all monsters. Your goal is to compute the minimum number of swings Ba Hong needs to defeat every monster.

Input

The first line contains three integers ~n~, ~p~, and ~q~ ~(1 ≤ n ≤ 2 · 10^5, 1 ≤ q ≤ p ≤ 10^9)~, representing the number of monsters, the damage dealt to the targeted monster, and the damage dealt to all other monsters, respectively.

The second line contains ~n~ integers ~a_1, a_2, ..., a_n~ ~(1 ≤ a_i ≤ 10^9)~, where ai is the initial hit-points of the monsters.

Output

Print a single integer: the minimum number of swings Ba Hong must perform.

Sample Input 1

2 3 2
5 5

Sample Ouput 1

2

Sample Input 2

3 5 3
17 13 14

Sample Ouput 2

5

On an experimental at UMT University, a smart bus system was designed to manage boarding and disembarking in an unusual way. At each stop, exactly half of the passengers on the bus - plus half a passenger (somehow) - get off.

This process continues identically for k consecutive stops. Remarkably, the bus is completely empty after the last stop, and no passenger was partially harmed or cut - the system somehow ensures integer behavior all along.

Given the number of stops k, can you determine the initial number of passengers n required such that the bus ends up empty under this strange pattern?

Input

The first line contains an integer ~T~ - the number of test cases.

Each of the following T lines contains a single integer ~k~ ~(1 ≤ k ≤ 30)~, the number of stops.

Output

For each test case, print the initial number of passengers n such that the bus becomes empty after exactly k stops.

Sample Input 1

2
1
3

Sample Ouput 1

1
7

In UMT University's "Algorithms for Strings", students are challenged to transform one string statistic into another. For an unknown string s of length n they are given its Z-function and must reconstruct the corresponding prefix-function (also called the ~π-array~ in KMP). Recall:

• ~Z[i]~ is the length of the longest substring starting at position ~i~ that is also a prefix (the first characters) of ~s~, here we consider the 0-index. Here we consider the proper (strict) substring so at position 0, we have ~Z[0] = 0~ (not taking the entire string). For example: "aaaaaa" - ~[0, 4, 3, 2, 1]~, "aaabaab" - ~[0, 2, 1, 0, 2, 1, 0]~, "abacaba" - ~[0, 0, 1, 0, 3, 0, 1]~.

• ~π[i]~ is the length of the longest proper prefix of the substring ~s[0..i]~ that is also its suffix.

Given all ~Z[i]~, you must output all ~π[i]~.

Input

The first line contains ~a~ single integer ~n~ ~(1 ≤ n ≤ 2 · 10^5)~ - the length of the string.

The second line contains ~n~ space-separated integers ~Z_0, Z_1, . . . , Z_{n-1}~ - the Z-function of the string.

Output

Print ~n~ integers - the prefix-function of the same string, separated by spaces.

Sample Input 1

8
0 0 1 0 3 0 1 1

Sample Ouput 1

0 0 1 0 1 2 3 1

Note: One string s that corresponding to the given Z-function is "ABACABAA".

During the final days of preparation for the entrance exam in Computer Science at UMT University, a student named Son Tan set a clear study goal: to accumulate a total of N units of knowledge. Each day, Son Tan studies M units consistently. This means that after each day, his total accumulated knowledge increases by exactly M units. Initially, Son Tan has no knowledge (i.e., his accumulated knowledge starts at 0).

To fully complete his goal, Son Tan wants the total required knowledge N to be divisible by M (i.e., ~N~ mod ~M = 0~). If this condition is already satisfied, everything is simple! However, if ~N~ is not divisible by ~M~, Son Tan allows himself to swap at most one pair of digits in the decimal representation of N to form a new number ~N'~. He wants to know whether such a single swap can result in a number divisible by ~M~.

You are given the integers ~N~ and ~M~. Determine whether it is possible to swap at most one pair of digits in ~N~ to obtain a new number that is divisible by ~M~. If N is already divisible by ~M~, print 0. If a swap is needed, print 1 ~i~ ~j~, where ~i < j~ are the indices of the digits to swap (with the smallest possible ~i~, and among those, the smallest possible ~j~). Indices are 0-based, counted from right to left. If no valid swap can make ~N~ divisible by ~M~, print -1.

Input

A single line containing two integers ~N~ and ~M~, representing Son Tan original goal and his daily progress. ~1 ≤ N ≤ 10^50000~ (i.e., ~N~ may have up to 50,000 digits) and ~1 ≤ M ≤ 10^9~

Output

The minimal solution according to the problem's requirements.

Sample Input 1

12539 4

Sample Ouput 1

1 0 3

Sample Input 2

13579 3

Sample Ouput 2

-1

Sample Input 3

1200 25

Sample Ouput 3

0

At UMT University, where technological ideas are always nurtured with passion and creativity, two outstanding members of the Computer Science Club An, a talented student, and Tiến, her brilliant friend, embarked on a new journey. During a practical simulation competition organized by the Faculty of Information Technology, they decided to collaborate on a project called "Cross the High Mountain."

The story unfolds in a remote highland village, where delivering mail isn't just a matter of moving between points, it's a challenge against the rugged terrain. An designed the village as a square matrix of size ~N × N~, where each cell represents an area with a specific altitude. Some cells are empty grassland ".", some are houses ~"A"~, and there is exactly one cell that represents the post office ~"T"~ the starting and ending point of the journey.

In the model An built, the mail carrier must start from the post office, visit all the houses to deliver mail, and then return to the post office. But instead of simply measuring distance like traditional models, Tiến introduced a more realistic metric: tiredness, defined as the difference between the highest and lowest altitude the carrier passes through during the entire trip. The carrier can move to adjacent cells in all 8 directions (including diagonals), but cannot traverse areas with altitudes outside a tolerable range. So, the challenge is to determine a route that visits all houses, returns to the post office, and minimizes the tiredness. This is not just an algorithmic problem, it's a challenge grounded in both realism and compassion. Now, An and Tiến are counting on you, their companion at UMT, to help solve this meaningful programming puzzle!

Input

The first line contains an integer ~N(2 ≤ N ≤ 50)~.

The next N lines describe the matrix representing the village. The character "T" appears exactly once (the post office), while the character "A" appears at least once (the houses).

The following N lines describe the altitude of each area in the matrix. Each altitude is a natural number not greater than 1,000,000.

Output

Print the smallest fatigue level on the first line.

Sample Input 1

3
A.T
...
A.A
3 3 4
9 5 9
8 3 7

Sample Ouput 1

5

Every morning, at UMT University, hundreds of buses transport students to their lecture halls. Each bus trip is defined by its start and end time, corresponding to when the first student is picked up and the last one is dropped off on that day, like the picture below.

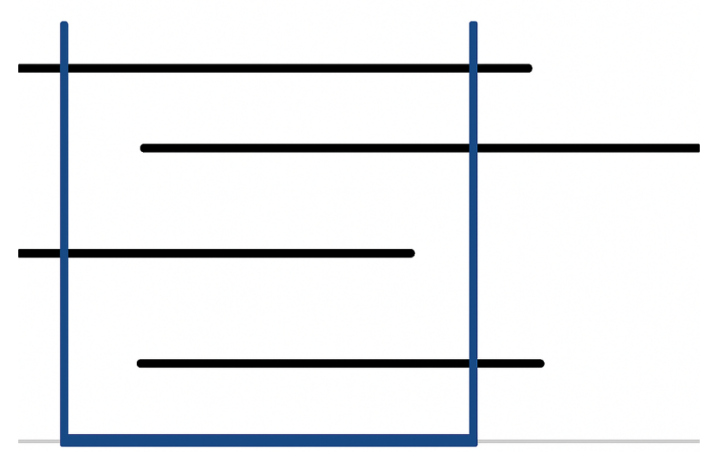
To optimize operating costs, the university administration wants to identify a main operating time window during which buses are active, in order to eliminate unnecessary expenses. Realizing that this problem could be solved through programming, a professor presented the following interesting challenge during a Computer Science Club meeting.

Find a time interval ~(A, B)~ such that the total active time of all bus trips that are completely contained within this interval is exactly K minutes. To simplify the task:

• If there are multiple valid pairs ~(A, B)~, choose the one with the smallest ~A~, and if there's a tie, the smallest ~B~.

• If no such interval exists, print 0 0.

Though the problem is simple in description, it requires precise time handling and efficient searching across a large dataset, a worthy challenge for all algorithm enthusiasts at UMT. Let's work together to solve it!

Input

The first line contains two integers ~N~ and ~K~ ~(1 ≤ N ≤ 10^3, 1 ≤ K ≤ 10^6)~.

The next ~N~ lines (from line 2 to line ~N + 1~) each contain two integers representing the left and right endpoints of a segment. Both endpoints are integers in the range ~0~ to ~10^6~.

Output

Print two integers, A and B. If no such pair exists, print "0 0".

If there are multiple valid pairs, choose the one with the smallest A. If multiple pairs share the same A, choose the one with the smallest B among them.

Sample Input 1

4 25
0 10
3 15
0 8
3 10

Sample Ouput 1

2 9

During a semester exam at UMT University, two students Phú, and Trung, were given a programming problem that simulates the internal infrastructure of the campus. The model is represented as a tree with ~N~ nodes, each node corresponding to a campus area such as a lecture hall, library, or laboratory. The connections between areas are modeled as edges, where each edge connects two nodes ~u_i~ and ~v_i~ and has an initial latency of ~w_i~.

The system must process ~Q~ queries, which fall into two types:

• Type 1 query: 1 ~i~ ~w~ - Phú updates the latency of the i-th connection (edge) to the new value ~w~.

• Type 2 query: 2 ~u~ ~v~ - Trung needs to calculate the total data transmission delay (i.e., the sum of edge weights) on the unique path from node ~u~ to node ~v~, ensuring efficient data flow between areas.

Meanwhile, Trung is responsible for verifying the output to ensure that every computation meets the problem's requirements. All queries are processed in order, and after each Type 2 query, the team must output the total delay along the current path between the two nodes.

Execute all queries in the given order. For each Type 2 query, print a single line containing the sum of weights on the path between the specified nodes ~u~ and ~v~.

Input

The first line contains an integer ~N~ ~(1 ≤ N ≤ 2 × 10^5)~, the number of nodes in the tree.

Each of the next N -1 lines contains three integers ~u_i~, ~v_i~, and ~w_i~ ~(1 ≤ u_i, v_i ≤ N, 1 ≤ w_i ≤ 10^9)~,describing the i-th edge connecting node ~u_i~ and node ~v_i~ with an initial weight (latency) of ~w_i~.

The next line contains an integer ~Q~ ~(1 ≤ Q ≤ 2 × 10^5)~ - the number of queries.

Each of the next Q lines contains a query in one of the following formats:

• 1 ~i~ ~w~ - Update the weight of the i-th edge to ~w~ ~(1 ≤ i ≤ N - 1, 1 ≤ w ≤ 10^9)~.

• 2 ~u~ ~v~ - Query the total weight on the path from node ~u~ to node ~v~ ~(1 ≤ u, v ≤ N)~.

It is guaranteed that there is at least one query of type 2.

Output

For each query of type 2, output a single line containing the total weight on the path from node ~u~ to node ~v~ at the time of the query.

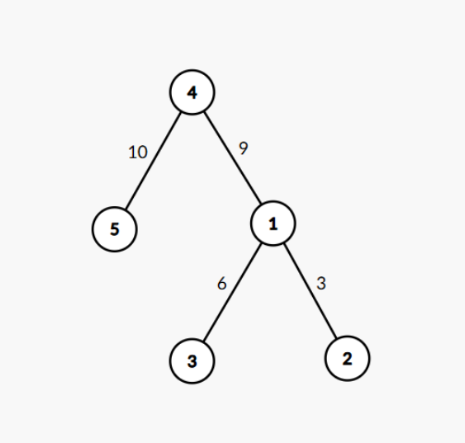
Sample Input 1

5
1 2 3
1 3 6
1 4 9
4 5 10
4
2 2 3
2 1 5
1 3 1
2 1 5

Sample Ouput 1

9
19
11

Note:

Each query should be processed in the given order.

• The first query asks for the distance between vertex 2 and vertex 3. The path from 2 to 3 goes through edge 1 and edge 2, with a total weight of 9, so the output should be 9.

• The second query asks for the distance between vertex 1 and vertex 5. The path goes through edge 3 and edge 4, with a total weight of 19, so the output should be 19.

• The third query updates the weight of edge 3 to 1.

• The fourth query again asks for the distance between vertex 1 and vertex 5. The updated path (edge 3 and edge 4) now has a total weight of 11, so the output should be 11.

At UMT University, the Computer Science Club recently held an exciting welcome activity for incoming freshmen, themed Conquering the Entrance Exam Challenge. In a lively atmosphere, the club advisor presented a thought-provoking problem for everyone to brainstorm and discuss together. The enthusiastic club members were given a special square grid C of size ~n×n~. Each row and column in the grid is numbered from 1 to ~n~. In addition, the students were provided with an array of ~n~ integers: ~a_1, a_2, ..., a_n~, representing the learning capabilities of each student in a group. Each cell ~(i, j)~ in the grid is assigned ~a~ value equal to ~a_i × a_j~ , that is, the product of the corresponding capabilities.

For example: with a sequence of 5 numbers ~a~ = (2, 4, 1, 5, 3) we have table C as shown below:

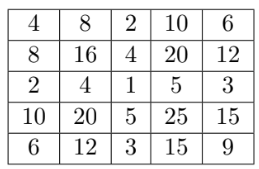
After filling in the grid, the advisor challenged everyone to figure out how many sub-rectangles in the grid have a total sum of exactly ~a~ given integer ~k~. A sub-rectangle is defined as a contiguous block of cells formed by a consecutive group of rows and a consecutive group of columns in the grid. As a future guiding star of the club, you are expected to apply your algorithmic thinking to solve this challenge!

Input

• The first line contains an integer ~n~ - the size of the grid ~(1 ≤ n ≤ 8000)~.

• The second line contains ~n~ integers ~a_1, a_2, ..., a_n (0 ≤ ai ≤ 100)~.

• The third line contains an integer ~k~ ~(1 ≤ k ≤ 10^6)~.

Output

Print a single line containing the number of sub-rectangles in the grid ~C~ whose sum of all elements is exactly ~k~.

Sample Input 1

5
2 4 1 5 3
30

Sample Ouput 1

12

The OLP-ICPC 2022 contest is the first time that UMT has participated. Under the guidance of Mr. Trung, the team has had memorable and rewarding experiences. After 2 more years of participation in Hue and Hanoi as well as exciting activities at the Algorithm Club, UMT's ICPC teams have significantly increased their fighting power. Recalling the intense review period, the UMT.Individual team shared a problem that was both strange and familiar, introduced by Mr.Trung, which left a lasting impression on them. That is a classic concept in programming: the Longest Increasing Subsequence (LIS).

You are given an array of integers ~A~ consisting of ~N~ elements. For each index ~i~ in the array, determine the following:

• The length of the longest increasing subsequence that ends at position ~i~.

• The length of the longest increasing subsequence that starts at position ~i~.

An increasing subsequence is a sequence of elements (not necessarily contiguous) from the original array, arranged in strictly increasing order (each element is greater than the one before it). The length of a subsequence is defined as the number of elements it contains.

Input

• The first line contains an integer ~N~ ~(1 ≤ N ≤ 10^6)~, the number of elements in the sequence.

• The second line contains ~N~ integers ~A_i~ ~(1 ≤ A_i ≤ 10^9)~, the elements of the sequence.

Output

The output consists of two lines, each containing ~N~ integers.

• The ~i^{th}~ number in the first line represents the length of the longest increasing subsequence ending at position ~i~.

• The ~i^{th}~ number in the second line represents the length of the longest increasing subsequence starting at position ~i~.

Sample Input 1

5
1 9 6 7 6

Sample Ouput 1

1 2 2 3 2
3 1 2 1 1

Note:

• At position 1, the longest increasing subsequences ending and starting here are: [1] and [1, 6, 7].

• At position 2, the longest increasing subsequences ending and starting here are: [1, 9] and [9].

• At position 3, the longest increasing subsequences ending and starting here are: [1, 6] and [6, 7].

• At position 4, the longest increasing subsequences ending and starting here are: [1, 6, 7] and [7].

• At position 5, the longest increasing subsequences ending and starting here are: [1, 6] and [6].