Để tạo niềm vui cho mọi người, chính quyền quyết định lắp đặt một thiết bị ở nơi công cộng. Thiết bị này giao tiếp với mọi người thông qua bàn phím và màn hình và có một số nguyên lưu bên trong bộ nhớ của nó. Ban đầu số nguyên này khởi đầu bằng 1.

Thiết bị hoạt động như sau:

• Một người gõ một số nguyên từ bàn phím

• Thiết bị sẽ nhân số trong bộ nhớ của nó với số nguyên vừa gõ và kết quả được lưu lại vào chính bộ nhớ này.

• Thiết bị sẽ hiển thị lời chào lên màn hình nếu như số trong bộ nhớ là số chính phương. Khi đó người gõ số sẽ được nhiều may mắn.

Yêu cầu: Viết chương trình, cho biết dãy số nguyên mà những người chơi lần lượt gõ, xác định xem người chơi nào sẽ là người may mắn.

Dữ liệu: File POTPUNI.INP

• Dòng đầu tiên chứa số nguyên N (1≤N≤500000) là số lượng người tham gia giao tiếp với thiết bị.

• Tiếp theo là N dòng, mỗi dòng ghi một số nguyên được gõ bởi một người theo thứ tự giao tiếp với thiết bị. Các số nguyên này nằm giữa 1 và ~10^6~.

*Chú ý rằng kết quả số trong bộ nhớ có thể vượt quá kiểu số nguyên 64 bit

Kết quả: File POTPUNI.OUT

Output ra kết quả mà mỗi người nhận được theo thứ tự. Ghi "DA" nếu kết quả là số chính phương và "NE" trong trường hợp ngược lại.

Sample Input

7
2
3
6
15
35
21
64

Sample Ouput

NE
NE
DA
NE
NE
DA
DA

Dưới đây là phiên bản đơn giản của một trò chơi phổ biến trong các nơi công cộng ở Bingo. Một cái máy lần lượt đọc các số nguyên và những người chơi sẽ tìm các số nguyên máy vừa đọc trên các tấm thẻ của họ.

Mỗi người chơi có một tấm thẻ được chia thành N hàng, N cột trong mỗi ô được gán một số nguyên trong phạm vi từ 1 đến N2, không có số nào được ghi hai lần.

Khi máy đọc, mỗi người chơi luôn kiểm tra N số cuối cùng máy vừa đọc. Nếu như N số này, theo thứ tự, trùng với 1 hàng của tấm thẻ thì người chơi được 1 điểm.

Ví dụ, giả sử N=3 và người chơi có tấm thẻ sau:

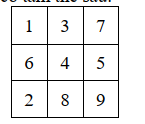
Nếu dãy số máy đọc là 7,1,3,6,4,5,7,1,2,2,8,9,3 thì người chơi được 2 điểm bởi vì hai dãy 6,4,5 và 2,8,9 xuất hiện như là 1 hàng trên thẻ của anh ta.

Yêu cầu:

Mirko muốn biết với cùng một dãy số mà máy đã đọc, số điểm lớn nhất của một tấm thẻ là bao nhiêu?

Dữ liệu: File BINGO.INP

• Dòng đầu tiên ghi hai số nguyên N, B (2 ≤ 𝑁 ≤ 4, 1 ≤ 𝐵 ≤ 10000) là kích cỡ của thẻ và số lượng các số mà máy đọc.

• B dòng tiếp theo mỗi dòng chứa một số theo thứ tự là dãy số mà máy đọc. Tất cả các số này nằm trong phạm vi từ 1 đến N2.

Kết quả: File BINGO.OUT

Một số nguyên là số điểm lớn nhất nhận được

Sample Input

2 11
1
2
1
2
1
2
1
2
3
4
1

Sample Output

5

Một ma trận vuông kích thước N x N được điền đầy bởi các số nguyên từ 1 đến ~N^2~ theo đường zig-zag. Ví dụ, với N=6 ta có ma trận dưới đây:

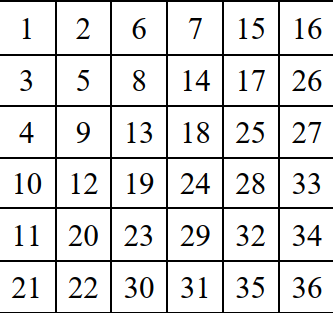
Có một robot đứng tại ô chứa số 1. Robot này có thể chuyển động theo 4 hướng (trên, dưới, trái, phải) đến ô khác chung cạnh nếu như ô này tồn tại.

Yêu cầu:

Cho dãy K lần chuyển động của robot. Viết chương trình xác định tổng của các số trong các ô mà robot đi qua (nếu một ô đi qua nhiều lần thì số trong ô này được cộng nhiều lần vào tổng)

Dữ liệu: File MATRIX.INP

• Dòng đầu tiên chứa hai số ngyên dương N và K (1≤N≤100000, 1≤K≤ 300000) lần lượt là kích thước của ma trận và số bước chuyển động của robot.

• Dòng thứ hai là dãy K ký tự 'U', 'D','L',R' mô tả các bước chuyển động ('U' - lên trên, 'D' - xuống dưới,'L' -sang trái,'R'-sang phải). Biết rằng với các hướng chuyển động này, robot không ra khỏi ma trận tại bất kỳ một bước nào.

Dữ liệu: File MATRIX.OUT

Một số nguyên dương là tổng các số trong các ô mà robot đi qua. Kết quả đảm bảo luôn là số nguyên 32 bit.

Sample Input 1

6 8
DDRRUULL

Sample Output 1

47

Sample Input 2

3 8
DDRRUULL

Sample Output 2

41

Sample Input 3

6 10
RRRRRDDDDD

Sample Output 3

203

Với sự chăm chỉ, những con kiến đã xây dựng được một thị trấn được gọi là thị trấn kiến. Thị trấn này xây dựng giống như một ma trận với H đường phố ngang và V đường phố dọc tạo thành VxH điểm giao cắt. Tất nhiên, loài kiến rất ghét nước nên mỗi khi có mưa thì thị trấn kiến trở nên hỗn loạn. Chính quyền thị trấn phải đặt một số cái dù ở một số điểm giao cắt để các con kiến trú ẩn. Tuy vậy chỉ có N điểm giao cắt được trang bị dù.

Khi bắt đầu mưa, tất cả các con kiến ở các ngã tư khác nhau bắt đầu chạy dọc theo các đường phố đến ngã tư gần nó nhất mà có dù. Tuy nhiên có một vài điểm giao cắt có nhiều hơn một điểm giao cắt có dù gần nó nhất. Những con kiến ở các giao cắt này sẽ không biết được cần phải chạy tới đâu do vậy chúng sẽ đứng yên và chịu ướt. Các điểm giao cắt như vậy được gọi là các điểm ướt.

Ví dụ, nếu thị trấn kiến có 10 đường phố ngang và 10 đường phố dọc, có 4 điểm giao cắt có ô thì các điểm có dấu '?' là các điểm ướt (hình dưới):

Yêu cầu:

Viết chương trình xác định số lượng các điểm ướt ở thị trấn kiến.

Dữ liệu: File MARVO.INP

• Dòng đầu tiên ghi hai số nguyên H và V là số lượng đường phố ngang và dọc của thị trấn kiến (1 ≤ 𝐻, 𝑉 ≤ 30000). Các đường phố ngang đánh số từ 1 đến H, các đường phố dọc đánh số từ 1 đến V.

• Dòng thứ hai chứa số nguyên N (1≤N≤10) là số lượng các điểm giao cắt có dù.

• N dòng tiếp theo, mỗi dòng ghi hai số nguyên h và v với ý nghĩa là tại điểm giao cắt hàng h với cột v có một cái ô

Dữ liệu: File MARVO.OUT

Một số nguyên duy nhất là số lượng các điểm ướt ở thị trấn kiến

Sample Input

10 10
4
4 4
4 6
6 4
9 9

Sample Output

19

Trong giờ học Nhập môn về lập trình, thầy Trung cho bạn Luna ba số nguyên ~a, b, c~ và một biểu thức có dạng sau đây

$$a (?) b (?) c (?)$$

trong đó ở mỗi vị trí ~(?)~, bạn Luna có thể điền vào một trong các dấu: cộng, trừ hoặc nhân. Rõ ràng mỗi vị trí có nhiều cách điền nên có thể sinh ra được nhiều kết quả khác nhau, bạn Luna muốn rằng giá trị của biểu thức tính được là càng lớn càng tốt. Chú ý rằng kết quả sẽ được tính theo thứ tự ưu tiên: nhân chia trước, cộng trừ sau và sẽ tính từ trái sang phải (không được thêm dấu ngoặc vào). Hãy giúp Luna chọn cách điền hợp lý và tìm được giá trị lớn nhất có thể.

Input

Dòng đầu tiên chứa 3 số nguyên ~a, b, c~. Biết ~|a|, |b|, |c| ≤ 10^5~

Output

Một dòng duy nhất là giá trị lớn nhất có thể đạt được.

Subtask

• Subtask 1 (50 điểm): Cả ba số ~a, b, c~ đều dương
• Subtask 2 (50 điểm): Không giới hạn gì thêm

Sample Input 1

19 6 7

Sample Ouput 1

798

Sample Input 2

3 2 -1

Sample Ouput 2

7

Giải thích

Ở test đầu tiên, bạn có thể điền vào giữa các dấu nhân để thu được kết quả 19 × 6 × 7 = 798.

Ở test sau, bạn có thể điền như sau ~3 × 2 - (-1) = 7~. Ta có thể kiểm tra được rằng không còn cách điền nào khác để thu được kết quả lớn hơn.

Tina và Luna hiện đang lạc trong một ma trận số vô cùng ký bí ở trong ngôi làng của mình. Biết rằng ma trận có kích thước ~NxN~ với các cột được đánh số từ trái qua phải, các hàng được đánh số từ trên xuống dưới, được mô tả với hình dưới đây:

Tuy tài trí hơn người là vậy nhưng khi đối mặt với những bài toán ma trận lại cực khó đối với cả hai. Và bạn là một người cực kỳ giỏi tin học để giúp vấn đề này. Luna cho bạn hai 2 số nguyên ~X~, ~Y~ biểu diễn hàng ~X~ cột ~Y~ nơi mà cả hai đang đứng bạn hãy cho biết giá trị của ô ~(X, Y)~ trong ma trận để cả hai có thể nhanh chóng thoát ra khỏi ma trận này.

Input

Dòng đầu tiên là một số nguyên N, ~(1 ≤ N ≤ 500)~ mô tả kích thước ma trận. Dòng tiếp theo chứa hai số nguyên ~X~, ~Y~ mô tả vị trí mà Tina và Luna đang đứng ~1 ≤ X~, ~Y ≤ N~.

Output

Một dòng duy nhất là giá trị ở ô mà cả hai đang đứng với ma trận kích thước ~N~ tương ứng.

Subtask

Vấn đề này chỉ có 1 Subtask là giới hạn đề bài.

Sample Input 1

2
2 1

Sample Ouput 1

2

Sample Input 2

1
1 1

Sample Ouput 2

1

Việc cân bằng giữa học tập, làm việc và giải trí, thư giãn không chỉ là bài toán khó của người trưởng thành mà cũng là của các genZ. Tuy nhiên, các sinh viên UMT luôn tiếp cận nó theo hướng rất thoải mái và hợp lý: học hết mình mà cũng chơi hết sức. Sau mỗi kỳ thi căng thẳng, các UMTer đều sẽ cùng nhau đi du lịch, trải nghiệm và chữa lành.

Lần này khu du lịch của các bạn có ~n~ địa điểm tham quan và các địa điểm đó nối nhau bởi ~n - 1~ con đường hai chiều sao cho từ địa điểm này đều có thể đi đến địa điểm khác thông qua các con đường. Các bạn muốn tham quan ở đây trong nhiều ngày, mỗi ngày sẽ xuất phát từ một địa điểm nào đó, đi qua các con đường đến các địa điểm khác mà thoả mãn các điều kiện sau đây:

• Mỗi con đường chỉ được đi qua đúng một lần (nhưng địa điểm thì có thể qua nhiều lần).
• Trong 2 ngày bất kỳ, nhóm bạn đều có cùng đến chơi tại ít nhất một địa điểm giống nhau.

Hỏi nhóm bạn UMTers có thể thực hiện chuyến đi thoả mãn yêu cầu trên không, và nếu được thì có thể đi chơi trong ít nhất và nhiều nhất bao nhiêu ngày?

Input

Dòng đầu tiên gồm số nguyên dương ~n~ với ~3 ≤ n ≤ 10^5~ cho biết số địa điểm (giả sử các địa điểm được đánh số từ 1 đến ~n~).

Trong ~n - 1~ dòng tiếp theo, mỗi dòng gồm một cặp số ~(a, b)~ với ~1 ≤ a, b ≤ n~ cho biết hai địa điểm thứ ~a, b~ có đường đi nối nhau.

Output

Nếu nhóm không thể thực hiện được chuyến đi thoả mãn thì in ra -1, ngược lại nếu có cách đi thì lần lượt in ra giá trị lớn nhất và nhỏ nhất của số ngày mà nhóm có thể tham quan, du lịch thoả mãn ràng buộc.

Sample Input 1

4
1 2
1 3
1 4

Sample Ouput 1

3 2

Sample Input 2

6
1 2
1 3
1 4
4 5
4 6

Sample Ouput 2

-1

Giải thích

Ở test đầu, nhóm có thể đi chơi trong ba ngày: ngày 1 đi từ ~1 → 2~, ngày 2 đi từ ~1 → 3~ và ngày 3 đi từ ~1 → 4~, lúc đó hai ngày bất kỳ đều có thăm chung địa điểm; hoặc nhóm chỉ đi trong hai ngày cũng được, ngày 1 đi từ ~2 → 1 → 3~ và ngày 2 đi từ ~1 → 4~.

Ở test sau, ta không có cách nào thực hiện được các chuyến đi chơi thoả mãn.